CHEZ L'HOMME/ANIMAL
Hypothèse:On suppose que l'on retrouve le nombre d'or chez les animaux
Résultats attendus : On retrouve phi chez les animaux
Les hypothèses,protocole et résultats attendus sont les mêmes pour tous les animaux suivants.
Le Lapin :
On considère qu’un couple de lapins arrive à maturité sexuelle à l’âge de deux mois et que chaque couple donne à chaque mois,naissance à un autre couple.On parle d’un seul couple de lapins . Soit (Fn) la suite defini par « Fn désigne le nombre de couple au bout du n-ième mois ».
On part d’un couple donc F(0)= 1
-au bout de 1er mois,le couple n’est pas encore arrivé à maturité sexuelle,on a donc toujours F(1)=1
-2ème mois ;le couple initial a atteint la majorité sexuelle donc nous avons +1 couple F(2)=2
-3ème mois ;le couple initial engendre un nouveau couple donc +1 couple mais pas de progéniture pour le deuxième couple car ils ne sont pas arriver à maturation sexuelle donc F(3)=3
-4ème mois ;Nous avons +1 du couple initial,+1 du second couple,mais pas pour le 3ème couple qui est trop jeune .Nous avons donc F(4)=5.
-5ème mois ;Sur les 5 couples,seul 3 d’entre eux sont à maturité sexuelle donc F(5)=8
-6ème mois ; Sur le même raisonnement F(6)=13 et ainsi de suite …
Mettons désormais en place un tableau :
|
N |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
Fn |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
Rappel : Soit N le nombre de mois et Fn ,le nombre de couple au bout du n-ième mois.
Faisons une pause et regardons le tableau :
On a F(0)=0 ;F(1)=1 ;F(2)=2 ;F(3)=3 ;F(4)=5 ;F(5)=8 ;F(6)=13
Essayons de comprendre la logique : 1,1,2,3,5,8,13.
1+1=2 ;1+2=3 ;2+3=5 ;3+5=8 ;5+8=13 ; donc logiquement le prochain devrait-être 8+13=21 puis 13+21=34.
On retrouve donc la suite de Fibonacci et sa relation dite de récurrence ,c’est-à-dire une suite définie par son premier terme et qui définit chaque terme à partir du précédent ou des précédents lorsqu'ils existent.



Les papillons :
Protocole : On calcule le rapport d1/d2 (voir schéma).
d1 est représente la distance de la bande jaune .
d2 représente la distance de la bande jaune+verte.
Résultats attendus : d1/d2= 1,618…
Expérience :Nous avons emprunté divers papillons provenant du laboratoire du lycée pour en mesurer d1 et d2 ,armé de règle et d’un compas (pour plus de précisions). Voici les données recueillis :
|
Noms papillons |
Vanessa |
Erebia Neoridas |
Ocolus pavonis |
Pièridès |
|
d1 |
0,8 cm |
0,4 |
0,5 |
0,4 |
|
d2 |
0,5 cm |
0,25 |
0,3 |
0,25 |
|
d1/d2 |
1,6 |
1,6 |
1,66… |
1,6 |
D’après nos résultats,le rapport de d1sur d2 est bien environ égal à 1,618…,notre hypothèse est donc validé.





Le Nautile/escargot
La construction de la coquille des escargots et du nautile ne sont pas sans rappeler la spirale d'or (dit logarithmique vu précédemment ).

Dans le cadre du nautile,ce dernier,vivant au tout début de sa vie dans le tout dernier compartiment (centrale) ,synthétise au fur et à mesure de sa vie une autre "chambre"similaire à celle initiale mais en plus grande où elle s'installe .Ce cycle se répète formant au final notre spirale d'or.




Autre
Voici d'autres exemples de la présence du nombre d'or chez les animaux grâce à l'utilisation d'une règle bien spéciale qui,en agrandissent un coté ,se règle automatiquement en fonction de phi de l'autre côté.
Nous avons ainsi la preuve de l'existence du nombre d'or sur les oiseaux,les plumes de paon,la fourmi ou bien la queue de lémuriens.

Nous faisons ces expériences pour savoir si nous avons le nombre d'or sur le corps humain.
1ère/ Expérience sur les doigts
Nous supposons que nous avons un nombre d'or dans les doigts, nous supposons donc que nos phalanges sont proportionnels au nombre d'or.
Protocole: Nous prenons un règle et nous relevons les résultats de chaque phalange. Puis nous divisons la première phalange à la deuxième et la deuxième à la troisième.
Nous représentons nos résultats (en cm) sous forme de tableau:
|
|
1ere phalange |
2eme phalange |
3e phalange |
1ere/2eme |
2eme/3eme |
|
Anou |
4,2 |
2,8 |
2,2 |
1,5 |
1,27 |
|
Alina |
4,4 |
3,0 |
2,05 |
1,57 |
1,46 |
|
Ingrid |
5,0 |
3,6 |
2,2 |
1,62 |
1,63 |
|
Célian |
5,50 |
3,5 |
2,258 |
1,57 |
1,55 |
|
Romain |
6,00 |
3,5 |
2,2 |
1,71 |
1,59 |
|
Adrien |
5,00 |
3,0 |
2,05 |
1,66 |
1,46 |
|
Alice |
5,50 |
3,3 |
2,32 |
1,66 |
1,42 |
|
Emilie |
5,60 |
3,2 |
2,02 |
1,75 |
1,58 |
|
Astrid |
5,20 |
3,20 |
2,01 |
1,62 |
1,59 |
|
Emma |
5,50 |
3,30 |
2,09 |
1,66 |
1,575 |
|
Ludivine |
5,50 |
3,20 |
1,96 |
1,71 |
1,63 |
|
Lorelei |
5,20 |
3,20 |
2,01 |
1,625 |
1,59 |
|
Théophile |
6,50 |
3,80 |
2,28 |
1,71 |
1,66 |
|
Gael |
5,50 |
3,30 |
3,32 |
1,66 |
1,42 |
|
Caroline J. |
5,70 |
3,30 |
2,09 |
1,72 |
1,575 |
|
Constance |
4,90 |
2,70 |
1,90 |
1,71 |
1,42 |
|
Claire |
5,20 |
3,50 |
2,30 |
1,48 |
1,52 |
|
Mr. Tannière |
5,90 |
3,70 |
2,60 |
1,59 |
1,42 |
|
Andréa |
5,00 |
3,00 |
1,93 |
1,66 |
1,55 |
|
Agathe |
5,30 |
3,00 |
1,88 |
1,76 |
1,66 |
|
Caroline G. |
5,18 |
3,10 |
1,94 |
1,64 |
1,59 |
|
Mazarine |
5,50 |
3,00 |
2,00 |
1,73 |
1,5 |
|
Elodie |
5,50 |
3,50 |
2,41 |
1,57 |
1,45 |
|
Kina |
5,00 |
3,00 |
1,92 |
1,66 |
1,56 |
|
Alexandre |
5,60 |
3,30 |
1,99 |
1,697 |
1,652 |
|
Joseph |
5,30 |
3,30 |
2,11 |
1,32 |
1,562 |
|
Amélie |
5,30 |
3,20 |
2,05 |
1,656 |
1,554 |
|
Mr. Louvrier |
6,20 |
3,80 |
2,30 |
1,63 |
1,65 |
|
Mme. Audant |
5,0 |
3,10 |
1,96 |
1,613 |
1,58 |
|
Gautier |
5,70 |
3,60 |
2,50 |
1,58 |
1,44 |
|
Pauline |
5,00 |
3,00 |
1,92 |
1,66 |
1,56 |
|
Laure |
5,80 |
3,20 |
1,95 |
1,81 |
1,64 |
CONCLUSION:
Nous remarquons que les résultats obtenus sont proches du nombre d'or, ainsi nous avons bien le nombre d'or dans nos doigts (il faut prendre en compte une marge d'erreur).
2ème/ Expérience au niveau de la tête
protocole: Nous prenons une règle et o relève les résultats de la hauteur de la tête, la largeur de la tête, la hauteurdu nez à la bouche et la hauteur du menton à la bouche. Puis nous divisons ces résultats:
hauteur de la tête = φ ; largeur de la tête= φ ; hauteur du nez à la bouche=φ .
largeur de la tête hauteur du nez hauteur du menton à la bouche
à la bouche
Les résultats obtenues sont représentés sous forme de tableau:
|
|
Hauteur de la tete |
Largeur de la tete |
Hauteur du nez à la bouche |
Hauteur du menton à la bouche |
hauteur de la tête largeur de la tête |
largeur de la tête hauteur du nez à la bouche |
hauteur du nez à la bouche hauteur du menton à la bouche |
|
Ingrid |
18,5 cm |
12 cm |
7,5cm |
4,20 cm |
1,625 |
1,6 |
1,78 |
|
Jacques chirac |
110 px |
70 px |
45 px |
27 px |
1.57 |
1.55 |
1.66 |
CONCLUSION:
Les résultats obtenus sont proches du nombre d'or, ainsi Jacques Chirac aurait une perfection cachée . Nous pouvons en conclure que le nombre d'or est bien présent dans le visage.








3ème/ Expérience au niveau des bras
protocole: Cette fois on relève les résultats de la coudée, paume, empan, palme et pied.
Puis, nous faisons la somme des résultats:
1) coudée= pied+empan; 2)pied= empan+palme; 3)empan= palme+paume
Expérience : On mesure sur chaque personne les élèments ci-dessus .
|
|
pied |
coudée |
empan |
palme |
paume |
1 |
2 |
3 |
|
Alina |
23 |
40,5 |
17 |
12 |
7 |
40 |
29 |
19 |
|
Ingrid |
25 |
40 |
11 |
15 |
8 |
36 |
26 |
13
|
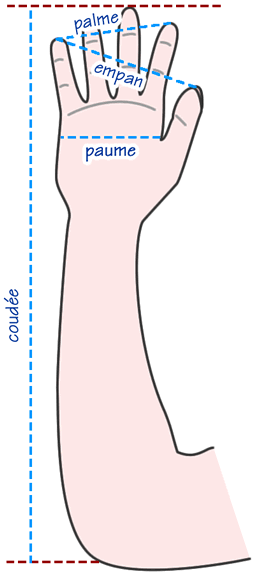
Conclusion: Les résultats obtenues sont proches de nos tailles réelles ainsi nous touchons le nombre d'or cependant il faut prendre en compte une marge d'erreur (du fait de l'imprécision des instruments utilisés).
4 ème expérience sur les dents :
Protocole:On divise la distance d1 sur la distance d2
Expérience: On présente les résultats sous forme de tableau
|
|
D1(cm) |
D2 (cm) |
D1 /D2 |
|
Cobaye 1 |
1,8 |
1,1 |
1 ,636 |
|
Cobaye 2 |
1,5 |
0,9 |
1,666 |
|
Cobaye 3 |
1,6 |
0,9 |
1,77 |
|
Cobaye 4 |
1,5 |
0,9 |
1,666 |
On observe que le rapport de d1 sur d2 équivaut un peu près au nombre d’or,on peut donc en conclure que phi se retrouve non seulement sur les doigts mais aussi dans la formation naturelle des dents.






